Trie 树
Trie 树(前缀树/字典树)是一种保存字符串的数据结构。它是一种树结构,除了根之外,节点都代表某个字符。将从根到某个节点的路径上的字符依次写下,就构成一个字符串。因此我们可以用 Trie 树判断一个字符串是否在一堆串中,或者判断一个字符串是否是某一个串的前缀。
我们用数组的形式表示 Trie 树,其中 trie[i][j] 就表示第 $i$ 个节点下属的字符 $j$ 的节点编号。
构建 Trie 树的时间复杂度是 $O(\sum |S|)$,即串长的和;空间复杂度是 $O(n|\Sigma|)$,即节点个数乘以字符总数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18int trie[100005][26] = {0}, cnt = 1;
bool isend[100005] = {0};
void insert(char *s){
int p = 1;
while (*s){
if (!trie[p][*s - 'a'])
trie[p][*s - 'a'] = ++cnt;
p = trie[p][*s - 'a'];
++s;
}
isend[p] = true;
}
bool Find(char *s){
int p = 1;
while (*s && p)
p = trie[p][*s - 'a'], ++s;
return p && isend[p];
}
Trie 树虽然原理简单,实现方便,但是却是一些高级数据结构的基础。
Manacher 算法
Manacher 算法可以用于求以所有可能的中心点扩展出的,最长回文串的长度。换言之,它是专门用来处理回文子串问题的算法。它的时间复杂度是线性的。
在介绍它之前,不妨对“回文子串”问题中的串做一个变形:向串中每一对相邻字符间都插入一个占位符(这里用 # 表示)。这样,我们就将偶数长度的回文情况转换成了奇数长度的回文情况(即变为以 # 为中心)。这样的推广带来了方便,因为下面我们可以只针对“以某个字符为中心的回文”这种情况讨论。
例如:
AABBAA变成A#A#B#B#A#A
Manacher 算法的特点在于它利用了隐藏的匹配信息。我们考虑下面这种情况:

图中黑色直线代表串,蓝色代表当前位置,红色代表到了蓝色位置时,右端点最靠右的回文串。可以发现,由回文串的性质,如果将蓝色位置以红色回文串的中心做一次对称,得到绿色位置,那么绿色位置向两侧延伸的情况应该是和蓝色位置一样。
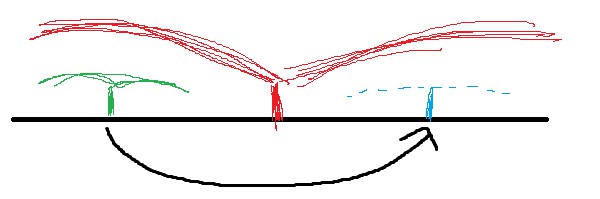
而在这之前,我们已经求出了以绿色位置的字符为中心的最长回文串。这样,我们就可以依照绿色位置的情况,直接先让蓝色位置的回文串向两侧延伸一段距离,然后再暴力判断蓝色位置的回文串是否能够延伸。
可以发现,这样一种对称的操作省略了以蓝色位置为中心时,向两侧延伸时的部分比较操作。实际上,因为最靠右的回文串的右端点是单调向右移动的,而只有暴力判断才会将右端点向右延伸,所以该算法最终的时间复杂度是线性的。
下面给出该算法的实现。具体实现中,并不向字符串中加入具体化的占位字符,而是用中心位置的下标加以区别:
- 如果下标是偶数就代表当前中心位置对应原字符串中的字符,解码方式是下标除以 2。
- 下标是奇数就代表当前中心位置是占位符,此时中心位置用原字符串中中心位置左右两个字符的位置表示,解码方式是下标除以 2 和 (下标除以 2 加 1) 分别对应原字符串这左、右两个字符。
(注:这个设定是针对于下标起始是 0 的时候)
另外一个细节是:对于每一个位置,求出的答案都是以该位置为中心的回文串的个数。使用个数这个设定比长度在某些情况下会更加方便。如果要使用长度作为目标函数,那么在程序的某些地方需要减掉一个 1。
有了这些前提,阅读下面这份代码就很容易了。
1 | /** |
必须指出,上述算法的实现虽然避免了加入填充字符的过程,但是效率却不如填充字符的版本。原因可能在于上述实现中运算量比较大。因此,在对时间复杂度要求较高而对于空间复杂度要求并不那么严格的场合,可以使用下面的实现。
1 | void manacher(char s[], char tmp[], int res[], int n){ |
KMP 算法
KMP算法的核心是后缀配对前缀,从而可以在配对失败的时候不用总是从头开始,而是从可以成功匹配的某一个前缀开始继续匹配。
KMP算法的匹配方式非常容易,但是需要预处理出一个next(或称fail)数组,表示匹配失败的时候跳转的位置。
若 $m$ 是模板的长度,$n$ 是文本串的长度,那么时间复杂度:$O(m+n)$,空间复杂度:$O(m)$。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24//构建fail数组
void build_fail(char *pat, int len, int *fail){
fail[0] = -1;
for (int i = 1, j = -1; i < len; ++i){
while (j > -1 && pat[i] != pat[j + 1])//j+1表示当前模板串内要匹配的前缀的字符
j = fail[j];
if (pat[i] == pat[j + 1])
fail[i] = ++j;
else
fail[i] = -1;
}
}
//匹配过程
void KMP_match(char *text, int l1, char *pat, int l2, int *fail){
for(int i = 0, j = -1; i < l1; ++i){
while(j > -1 && text[i] != pat[j + 1])
j = fail[j];
if(text[i] == pat[j + 1])
j++;
if(j == l2 - 1){
//do something... 因为你已经匹配到了。
}
}
}
扩展 KMP 算法(Z 算法)
定义 Z 函数:对于串 $S[0…n), T[0…m)$,$z[i]$ 表示 $S[i…n)$ 和 $T$ 的最长公共前缀。我们希望有一个算法,能够求出每一个位置上的 Z 函数。
这个定义和名字有一些关系:因为如果 $\exists i, z[i]=m$,那么就表明 $T$ 在 $S$ 中出现过。这和 KMP 算法的目标是一样的,所以一般称该算法为扩展 KMP 算法。
要求 Z 函数,$O(n^2)$ 的暴力是容易实现的。我们考虑像 KMP 算法一样利用一些有用的信息。先假设我们已经求出了 $z[0…i)$,现在我们要求 $z[i]$。类比 Manacher 算法的思想,我们考虑某一个位置 $p = \arg \max (i+z[i]-1)$。它的直观意义是和 $T$ 相匹配时延伸到最右的,$S$ 的某个后缀的起始位置。同样,我们讨论 $p$ 和 $i$ 的关系:(方便起见,下面设 $r=p + z[p]-1$)
- $i > r$。这时,我们似乎不能得到任何的有效信息,于是只有通过暴力匹配计算 $z[i]$。
$i \le r$。这时,通过匹配关系,我们可以得出:$S[p…r] = T[0…r-p]$。那么 $S[i…r] = T[i-p…r-p]$。这件事似乎并没有说明什么,因此我们不妨先考虑一个特殊情况:$S=T$。假设我们已经求出来了这种情况下的 Z 函数数组,并设其为 next。(这里和 KMP 中的在定义上稍微有些不同)
回到一般情况,我们可以用上述 next 数组方便求解。考虑 $next[i-p]$,设其为 $l$。则:
- $l \le r-i$。那么直接令 $z[i]=l$。因为如果 $z[i]>l$,那么至少存在 $l’>l$,使得 $S[i…i+l’)=T[0…l’)=T[i-p…i-p+l’)$。而根据 next 数组的定义,这表明 $next[i-p]>l$,矛盾。
- $l >r-i$。那么先令 $z[i]=l$,而在 $S[r]$ 之后的情况就完全不清楚了,所以这时候直接从 $S[r+1]$ 开始暴力匹配,并且更新 $p$ 和 $r$。
在 $S=T$ 时,我们可以使用之前已经得到了的 next 数组求解剩余部分。这样,我们可以先对 $T$ 自身做一次扩展 KMP(相当于预处理),然后再对 $S$ 做一次。
和对 Manacher 算法分析时间复杂度的过程类似,可以证明两种情况下的时间复杂度都是线性的。所以整个扩展 KMP 的时间复杂度是线性的。
下面给出一个简单的实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32void exKMP(char s[], char t[], int n, int m, int nxt[], int z[]){
nxt[0] = m;
int j = 0, p = 1;
while (j + 1 < m && t[j] == t[j + 1])
++j;
nxt[1] = j;
for (int i = 2; i < m; ++i) {
int r = p + nxt[p] - 1, l = nxt[i - p];
if (l <= r - i) nxt[i] = l;
else {
j = max(0, r - i + 1);
while (j + i < m && t[j] == t[j + i])
++j;
nxt[i] = j, p = i;
}
}
j = 0, p = 0;
while (j < n && j < m && s[j] == t[j])
++j;
z[0] = j;
for (int i = 1; i < n; ++i){
int r = p + z[p] - 1, l = nxt[i - p];
if (l <= r - i) z[i] = l;
else {
j = max(0, r - i + 1);
while (j + i < n && j < m && t[j] == s[j + i])
++j;
z[i] = j, p = i;
}
}
}
上述代码将 $i>r$ 和 $l >r-i$ 的情况做了整合。
最小表示法
给定串 $S[0…n)$,设 $T(i)=S[i…n) + S[0…i)$。设字典序意义下 $\min T(i)$ 为 $S$ 的最小表示。
最简单的求最小表示的方法是暴力,在数据随机的情况下暴力表现很好,但是在串中有大量重复子串的时候,暴力的时间复杂度退化到 $O(n^2)$。
我们针对这种情况优化。考虑两个不同的数 $i, j$,设 $T(i), T(j)$ 的前 $k$ 个字符相同,当到达 $k+1$ 个字符的时候:
- $T(i)[k] > T(j)[k]$。那么对于所有的 $l\in [i…i+k]$,$T(l)$ 必然不能成为答案,因为此时 $T(j+l-i)$ 必然比其更优。
- $T(i)[k] < T(j)[k]$。那么对于所有的 $l\in [j…j+k]$,$T(l)$ 必然不能成为答案,因为此时 $T(i+l-j)$ 必然比其更优。
- $T(i)[k] = T(j)[k]$。那么 $k:=k+1$,继续比较。
可以发现,无论是哪一种情况,都要么为之后排除一部分选项做了准备,要么直接排除了一部分选项。因为选项至多有 $n$ 个,所以我们可以设计一个算法,让这 $n$ 个选项相互比较、排除。算法的实现如下:
1 | int minrep(char *s, int n){ |
该算法基本按照上述原理实现。最后返回的是 $i$ 和 $j$ 的最小者,这是因为若整个字符串全部由同一种字符构成,则返回 $0$ 是比较好的选择;否则 $k$ 必然小于 $n$,这时 $i$ 和 $j$ 必然有一个越界,因此我们选择较小的那个也就是选择了没有越界的那个。
例题:HDU 2609