模板 数学（1）

一些简单的数学相关算法模板。
本文主要集中于快速幂和快速乘，与质数相关的问题。

快速幂

对于 $a^b$，把 $b$ 展开成为二进制形式，然后按位乘，同时让 $a$ 反复平方。

时间复杂度：$O(\log n)$

int modpow(int a, int b, int M){
    int res = 1;
    while(b){
        if(b & 1) res = (res * a) % M;
        a = (a * a) % M, b >>= 1;
    }
    return res;
}

特化版本：

//模数比较大，但是平方不会爆long long时
int modpow(int a, int b, int M){
    int res = 1;
    while(b){
        if(b & 1) res = 1ll * res * a % M;
        a = 1ll * a * a % M, b >>= 1;
    }
    return res;
}
//模数很大，很容易爆long long时
ll modpow(ll a, ll b, ll M){
    ll res = 1;
    while(b){
        if(b & 1) res = fstmul(res, a, M);
        a = fstmul(a, a, M), b >>= 1;
    }
    return res;
}

---

快速乘

实现一

当 $a\times b \bmod M$ 可能超过当前类型限制时，可以将 $b$ 展开成为二进制，然后根据乘法分配律让 $a$ 按位乘，即可避免溢出。

时间复杂度：$O(\log n)$

int fstmul(int a, int b, int M){
    int res = 0;
    while(b){
        if(b & 1) res = (res + a) % M;
        a <<= 1, a %= M, b >>= 1;
    }
    return res;
}

特化版本：

//模数很大时
ll fstmul(ll a, ll b, ll M){
    ll res = 0;
    while(b){
        if(b & 1) {
            res += a;
            if(res >= M) res -= M;
        }
        a <<= 1, b >>= 1;
        if(a >= M) a -= M;
    }
    return res;
}

实现二

因为 $a\times b \bmod M = a\times b - \lfloor \frac{a\times b}{M} \rfloor \times M$，因此可以用(long) double来存 $\frac{a\times b}{M}$，然后再化成整数去乘 $M$，再算出对应的结果。

时间复杂度：$O(1)$

int fstmul_2(int a, int b, int M){
    int c = (double)a * b / M;
    int res = (a * b - c * M) % M; //此时res由于溢出，可能为负数
    if(res < 0) res += M;
    return res;
}

特化版本：

//模数是long long级别
ll fstmul_2(ll a, ll b, ll M){
    ll c = (long double)a * b / M;
    ll res = (a * b - c * M) % M; //此时res由于溢出，可能为负数
    if(res < 0) res += M;
    return res;
}

---

素数定理

$$\pi(x) \sim \frac{N}{\ln N}$$

可以用这个定理估计一定范围内的素数个数。

---

质数判断

试除法

一个数 $N$ 为合数，那么一定有一个数 $T$，使得 $T|N,2\le T \le \sqrt{N}$。根据这个可以用时间复杂度 $O(\sqrt n)$ 判断质数。

bool isP(int x){
    if(x <= 1) return false;
    for(int i = 2; i * i <= x; ++i)
        if(x % i == 0) return false;
    return true;
}

特化版本：

//x比较大，long long级别
bool isP(ll x){
    if(x <= 1ll) return false;
    for(ll i = 2; i * i <= x; ++i)
        if(x % i == 0) return false;
    return true;
}

Miller-Rabin算法

由费马小定理，当 $p$ 为一个质数，对于 $gcd(a, p) = 1$，有 $a^{p - 1} \equiv 1 \pmod p$。反过来说，当我们知道有 $gcd(a, p) = 1$，并且 $a^{p - 1} \equiv 1 \pmod p$ 时，那么 $p$ 就有可能是质数。

理论上，要认定一个数 $p$ 为一个质数，我们可以用所有小于它的和它互质的数 $a$ 做一个判定，即判断是否有 $a^{p - 1} \equiv 1 \pmod p$。如果全部成立，那么 $p$ 几乎就是一个质数。之所以说是几乎，是因为存在这样的合数——卡迈克尔数（Carmicheal Number），其可以通过上述的判定，但却是合数。因此，必须要做出一些改进，使得判定更为准确。

下面先直接给出 Miller-Rabin 算法的代码：

bool witness(int a, int n, int t, int u){
    int x = modpow(a, u, n);
    if (x == 1 || x == n - 1)
        return false;
    for(int i = 0; i < t; ++i){
        int xx = (x * x) % n;
        if(xx == 1 && x != 1 && x != n - 1)
            return true;
        x = xx;
    }
    if(x != 1) return true;
    return false;
}
bool isP_miller_rabin(int n, int times){//执行times次
    int t = 0, u = n - 1;
    while(!(u & 1)) ++t, u >>= 1;
    while(times--){
        int a = rand() % (n - 1) + 1;
        if(witness(a, n, t, u)) return false;
    }
    return true;
}

该算法的另一个理论基础是二次探测定理：若 $x^2 \equiv 1\pmod p$，$p$ 为质数，那么 $x\equiv 1 \pmod p$ 或者 $x \equiv -1 \pmod p$。这是因为上式可以化成 $(x+1)(x-1)\equiv 0 \pmod p$，而 $p$ 是一个质数，由质数的锐利性质（即 $p|ab\implies p|a \vee p|b$）可得。

当 $p$ 为质数时，令 $p-1= 2^tu$，那么对于序列 $a^u, a^{2u}, a^{2^2u}, …, a^{2^tu}$，由于最后一项一定为 $1$，那么必然有以下条件中的一个：

1. $a^u \equiv 1 \pmod p$
2. $\exists i \in \lbrace 0, 1, 2, … , t-1\rbrace, a^{2^iu} \equiv -1 \pmod p$

若这两个性质都不符合，那么就能够确认 $p$ 是合数。可以证明，这样的 $a$ 占了 $1$ 到 $p-1$ 的 $75\%$ 左右，因此做 $T$ 次判断，失误率近似在 $4^{-T}$。

要取得更加优秀的结果，可以先根据质数表，看看几个小质数是不是程序中 $n$ 的因子，然后再进行 Miller-Rabin 验证。还有一种优化思路是减少 witness 的次数。有一种说法是：对于 32 位整数，只需要选取最小的 4 个质数作为验证的 $a$ 即可；对于 64 位整数则为最小的 12 个质数。

特化版本：

ll prime[] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};
bool witness(ll a, ll n, ll t, ll u){
    ll x = modpow(a, u, n);
    if (x == 1 || x == n - 1)
        return false;
    for(ll i = 0; i < t; ++i){
        ll xx = fstmul(x, x, n);
        if(xx == 1 && x != 1 && x != n - 1)
            return true;
        x = xx;
    }
    if(x != 1) return true;
    return false;
}
bool miller_rabin(ll n){
    for(int i = 0; i < 12; ++i)
        if(n % prime[i] == 0){
            if(n == prime[i]) return true;
            return false;
        }
    ll t = 0, u = n - 1;
    while(!(u & 1ll)) ++t, u >>= 1;
    for(int i = 0; i < 12; ++i)
        if(witness(prime[i], n, t, u)) 
            return false;
    return true;
}

---

求质数

埃氏筛法

基于“合数一定有一个大于 $1$，小于自身的质因数”的想法，可以直接从 $2$ 向 $n$ 扫描，遇到没有被标记的数就认为它是质数，然后把它的倍数全部标记。这样没有被标记的数就全部都是质数了。

由于遇到一个质数 $p$ 的时候小于 $p^2$ 的 $p$ 的倍数已经全部被标记了，所以可以直接从 $p^2$ 开始进行筛除。

时间复杂度：$O(n\log \log n)$。（小于 $n$ 的质数的倒数和约为 $\log \log n$，参见此处）

void getP(int N){
    for(int i = 2; i <= N; ++i)
        if(!vis[i]){
            for(int j = i * i; j <= N; j += i)
                vis[j] = 1;
        }
}

区间筛法

要筛出 $[L, R]$ 上面的质数，只需要筛出所有 $[2, \sqrt{R}]$ 上面的质数即可，因为 $[L, R]$ 上面的合数必然有一个位于 $[2, \sqrt{R}]$ 上面的质因子。

时间复杂度：$O((R-L) \log \log R)$（基于埃氏筛法）

void getP(int L, int R){
    if(L <= 1) L = 2;
    for(int i = 1; i <= cnt; ++i){
        unsigned int p = prime[i];
        if(R < p) break;
        for(unsigned int j = max((L - 1 + p) / p, 2u); j <= R / p; ++j)//这里取j的初始值是为了保证能取到区间内所有p的倍数
            vis2[j * p - L] = 1;
    }
}

欧拉筛法

也称线性筛法。观察上面的埃氏筛法程序容易发现，一个数常常会被多个质数筛掉，这样会影响效率。如果一个数只会被筛一次，那么就可以做到线性的时间复杂度。

考虑每一个数的最小质因数 $mindiv[i]$，从 $2$ 到 $n$ 扫描。如果一个数未被访问过，那就把它加入质数里面。然后对于当前的数 $i$，利用所有小于或者等于 $mindiv[i]$ 的质数 $p$，标记 $mindiv[i]\times p$ 为合数，同时置其最小质因数为 $p$。这样每一个合数就都被它的最小质因数筛掉了。

时间复杂度：$O(n)$。

// 本代码未显式保存mindiv
int prime[N >> 1], tot = 0;
bool vis[N];
void getP(int N){
    for (int i = 2; i <= N; ++i){
        if (!vis[i])
            prime[tot++] = i;
        for (int j = 0; j < tot; ++j){
            if (i * prime[j] > N) break;
            vis[i * prime[j]] = 1;
            if (i % prime[j] == 0) 
                break; 
            // 这一步起到的是让p不大于最小质因数
        }
    }
}

---

质因数分解

算术基本定理

对于任何一个大于 $1$ 的正整数 $n$，$n$ 都能被唯一分解为有限个质数的乘积，写作：

$$n = p_1^{c_1} p_2^{c_2} \cdots p_m^{c_m}$$

其中 $c_i \ge 1$、$p_i$ 是质数 $(\forall i)$，且 $p_1<p_2< \cdots <p_m$。

试除法

实现上和判断质数差不多，原理上和埃氏筛法相似。令 $i$ 从 $2$ 到 $\sqrt n$ 扫描，如果 $i\mid n$，那么就一直除到 $i \nmid n$，然后记录对应的质因子及次数。时间复杂度：$O(\sqrt n)$。

void getPs(int x){
    int t = x;
    for(int i = 2; i * i <= x; ++i){
        if(t % i == 0){
            do{
                //do something...
                t /= i;
            }while(t % i == 0);
        }
        if(t == 1) break;
    }
    if(t != 1){
        //do something...
    }
}

Pollard’s Rho算法

Pollard’s Rho算法是一种不太完美，但却比较快的算法。它基于生日悖论：因为一个合数 $n$ 必然有一个质因子 $p$ 满足 $p\le \sqrt n$，所以在选择 $n^{\frac 1 4}$ 个随机数时，就有比较大的概率（大约 $50\%$）得到这样一个 $p$。而Rho算法对此做出了一些改进，使得得到 $p$ 的概率增加：它不局限于寻找 $p$，而是对 $p$ 的倍数也加以关注。它选取一系列随机数 $\left\{ x_n\right\}$，看是否有 $n>\gcd(x_i-x_j, n)>1$，如果有就说明找到了这样一个因子。

Rho算法生成随机数时使用了一个函数 $f(x)$，它的一般形式是 $f(x)=(x^2+c)\bmod n$。用这样的函数生成的序列具有一定的随机性，但是也会存在闭环的问题，即从一个数开始生成后，在某一处得到的数在这之前已经生成过，那么之后生成的序列就和之前的一段相同了。把这样的序列写出来，就和字母 $\rho$ 一样。

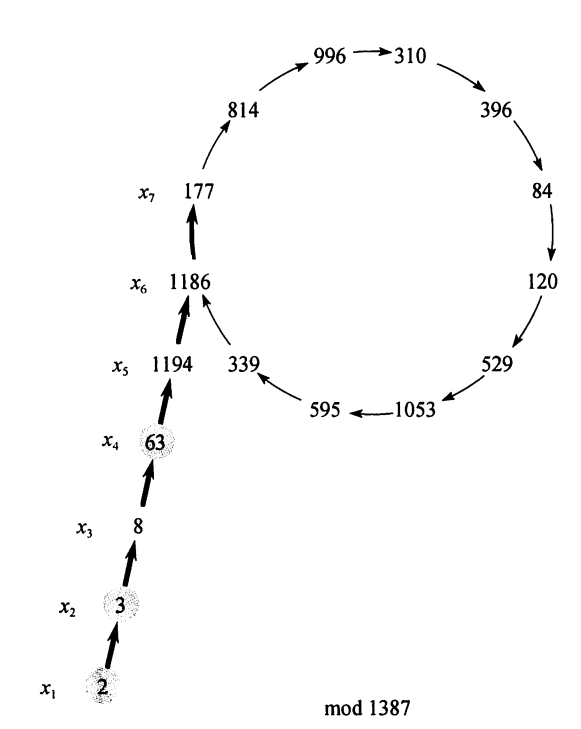
如果此时仍然没有找到一个质因子，那么本次寻找失败。

要判断环的出现有 2 种算法，一种是广为人知的 Floyd 判环算法，另一种则是 Brent 的判环算法。后者的表现要优于前者。这里的代码基于后者实现：

int rho(int n, int c){
    int x = modpow(rand(), rand(), n);
    int y = x, k = 2, d = 1;
    for(int i = 1; d == 1; ++i){
        x = modpow(x, x, n) + c;
        if(x > n) x -= n;
        d = gcd(abs(x - y), n);
        if(i == k) y = x, k <<= 1;
    }
    return d;
}
int Pollard(int n){
    int d = n;
    while(d == n)
        d = rho(n, rand() % (n - 3) + 3);	
    return d;
}

还可以对上述算法进行优化（这个优化基于这篇论文）。

我们知道，如果 $\gcd(a, c) > 1$，那么 $\gcd(ab, c) > 1(b>0)$。由辗转相除法：$\gcd(ab\bmod c, c) > 1(b>0)$。利用这一点，我们可以减少 gcd 函数的调用次数。只需要将每一次产生的 $|x-y|$ 乘起来（这一步可以称为积累因子），然后经过一定的迭代轮数再对这个乘积和 $n$ 求最大公约数。这么做可以大大的增加算法的效率。

ll rho(ll n, ll c){
    ll x = rand();
    ll y = x, d = 1, q = 1;
    for(int k = 2; d == 1; k <<= 1, y = x, q = 1){
        for(int i = 0; i < k; ++i){
            x = fstmul(x, x, n) + c;
            if(x >= n) x -= n;
            ll Abs = (x > y) ? x - y : y - x;
            q = fstmul(q, Abs, n);//这一步是保证因子的积累

            if(i >= 128 && (!(i & 31))){
                d = gcd(q, n);
                if (d > 1) return d;
            }
        }
        d = gcd(q, n);
    }
    return d;
}

时间复杂度：$O(n^{\frac 1 4})$（最好情况下）

---

求第 $n$ 个质数

基本方法

筛到第 $n$ 个为止。

黑科技

我们使用 Meissel-Lehmer 算法在 $O(n^{\frac 2 3})$ 的时间复杂度内求出第 $n$ 个质数。

---

积性函数

积性函数的值也可以用筛法求出。

线性筛

线性筛可以在线性时间内求出一段区间内的积性函数值。对于这个函数 $f$，只需要调整四个地方即可：

1. 确定 $f(1)$。实际上这一步并不在筛的过程中完成。
2. 当 $p$ 是质数时，直接算出并且填入 $f(p)$。
3. 在内层循环中，设质数是 $p$，当前数是 $x$，那么如果 $p|x$，考虑 $f(px)$ 的值如何取；
4. 如果 $p\nmid x$，考虑 $f(px)$ 的值如何取。

以 $f(x)=\sum_{i=1}^{x} [i\mid x]$（即 $x$ 的约数个数）为例：有关系式

$$f(x) = \begin{cases} 2 & \text{if } x \text{ is a prime} \\ f(p)f(\frac{x}{p}) & \text{if } p^2\nmid x \\ \frac{e+2}{e+1} f(p)f(\frac{x}{p}) & \text{if } p^2\mid x \\ \end{cases}$$

上式中的 $e$ 表示 $\frac{x}{p}$ 中 $p$ 的次数，需要额外维护。这样就不难写出程序：

int f[100005], prime[50005], tot = 0, mine[100005] = {0};
bool vis[100005] = {0};
void getf(int N){
    f[1] = 1;
    for(int i = 2; i <= N; ++i){
        if(!vis[i])
            prime[++tot] = i, f[i] = 2, mine[i] = 1;
        for(int j = 1; j <= tot; ++j){
            ll t = 1ll * i * prime[j];
            if(t > 1ll * N) break;
            vis[t] = true;
            if(i % prime[j] == 0){
                f[t] = f[i] * f[prime[j]] / (mine[i] + 1);
                f[t] *= mine[i] + 2;
                mine[t] = mine[i] + 1;
                break;
            }else{
                f[t] = f[i] * f[prime[j]];
                mine[t] = 1;
            }
        }
    }
}

有时候考虑 $f(p^k)$ 可能会比上面那个过程更方便。这里其实就是用了唯一分解定理，对每一个 $p^k$ 求出其函数值，然后乘起来就得到 $f(n)$。

对于其他常见的积性函数有：

线性筛约数和函数

定义为 $f(x)=\sum_{d\mid x} d$。相关式子为：

$$f(x) = \begin{cases} x+1 & \text{if } x \text{ is a prime} \\ f(p)f(\frac{x}{p}) & \text{if } p^2\nmid x \\ \frac{p^{e+2}-1}{p^{e+1}-1} f(\frac{x}{p}) & \text{if } p^2\mid x \\ \end{cases}$$

上式中的 $e$ 表示 $\frac{x}{p}$ 中 $p$ 的次数，需要额外维护。

int f[100005], prime[50005], tot = 0, mine[100005] = {0};
bool vis[100005] = {0};
void getf(int N){
    f[1] = sum = 1;
    for(int i = 2; i <= N; ++i){
        if(!vis[i])
            prime[++tot] = i, f[i] = i + 1, mine[i] = i * i - 1;
        for(int j = 1; j <= tot; ++j){
            ll t = 1ll * i * prime[j];
            if(t > 1ll * N) break;
            vis[t] = true;
            if(i % prime[j] == 0){
                mine[t] = (mine[i] + 1) * prime[j] - 1;
                f[t] = f[i] * mine[t] / mine[i];
                break;
            }else{
                f[t] = f[i] * f[prime[j]];
                mine[t] = prime[j] * prime[j] - 1;
            }
        }
    }
}

线性筛欧拉函数

线性筛莫比乌斯函数

---

参考资料

1. 维基百科
2. 《算法竞赛进阶指南》
3. 《算法导论》
4. 《数论概论》
5. 论文Computing π(x): The Meissel-Lehmer Method