模板 卷积变换

发表于 | 分类于 |
字数统计: 2,304 字

本文主要讨论三个算法：FFT，NTT 和 FWT。

基础知识

卷积

在泛函分析中，卷积、叠积（convolution）、摺积或旋积，是通过两个函数 $f$ 和 $g$ 生成第三个函数的一种数学算子，表征函数 $f$ 与经过翻转和平移的 $g$ 的乘积函数所围成的曲边梯形的面积。如果将参加卷积的一个函数看作区间的指示函数，卷积还可以被看作是“移动平均”的推广。

————维基百科

事实上，在这里我们主要讨论的是定义在数列上的卷积。最基本的一个问题是：

给定两个长度有限的序列 ，求出序列 ，使得 ，其中 $\oplus$ 是某个满足交换律的二元运算。

复数单位根

根据代数基本定理，复数方程 $z^n = 1$ 有 $n$ 个根，这些根互不相同，可以表示为 $e^{\frac{2\pi k i}{n}} = \cos(\frac{2\pi k }{n})+i\sin(\frac{2\pi k }{n})\quad (k\in \lbrace 0, 1, \cdots, n- 1 \rbrace)$。一般记作 。

单位根具有一些很神奇的性质：

  1. 。
  2. 各不相同。
  3. 。这一个性质有着很强的几何意义。
  4. 。
  5. 。特别地，。

原根和阶

该部分内容会在 NTT 相关材料中涉及到。

FFT（快速傅里叶变换）

基础：离散傅里叶变换

离散傅里叶变换（DFT）是 FFT 的基础。

我们知道，一般我们表示多项式都是采用系数表示，即给出多项式的次数 $n$ 和一个序列 ，那么这个多项式就是 。而 DFT 做的事情就是将一个给定多项式的系数表示转换成为点值表示（这个过程称为求值）。所谓一个多项式的点值表示，就是指一个 $n-1$ 次多项式可以用 $n$ 个不同的多项式函数图像上的点来表示。我们可以解方程求出这 $n$ 个点对应的 $n-1$ 次多项式，这表明了多项式和其点值表示是一一对应的。

一般的求值方法是选出任意 $n$ 个不同的横坐标，然后代入计算。这样的时间复杂度是朴素的 $O(n^2)$。由于横坐标可以任取，我们考虑取一些特殊的横坐标以优化求值过程。而这里“特殊的横坐标”就是 $z^n=1$ 的 $n$ 个单位根。

（方便起见，我们事先约定：$n$ 是 $2$ 的某一个正整数次幂。下面和长度有关的叙述基本继承这个设定，除非特殊说明）

考虑 $n -1$ 次多项式 。我们将其分为 ，并令等号右侧中，左边的多项式为 $G(x)$，右边的多项式为 $H(x)$。那么显然有 $F(x) = G(x^2) + xH(x^2)$。

令 $k<n/2$，代入 ，有 。那么

令 $k<n/2$，代入 ，有 。那么

显然，上面的式子具有很强的子结构性质，我们考虑递归分治求解。如果我们已经求出了 $G(x), H(x)$ 的点值表示，那么显然我们可以在 $O(n)$ 时间内求出 $F(x)$ 的点值表示。整个过程的时间复杂度是 $O(n\log n)$。

蝴蝶变换

有一个细节值得考虑：每一次 $F(x)$ 分裂为 $G(x)$ 和 $H(x)$ 时，$F(x)$ 的系数会按照奇偶性分配给 $G(x)$ 和 $H(x)$。

这是采用自顶向下视角，在子过程开始时所看到的现象。如果我们一层一层地画出系数的位置是如何变化的（即系数是怎么分配的），就会发现一种奇妙的对应：整个过程中，最顶层的系数下标，和与其对应的最底层的系数下标，呈二进制反转关系。

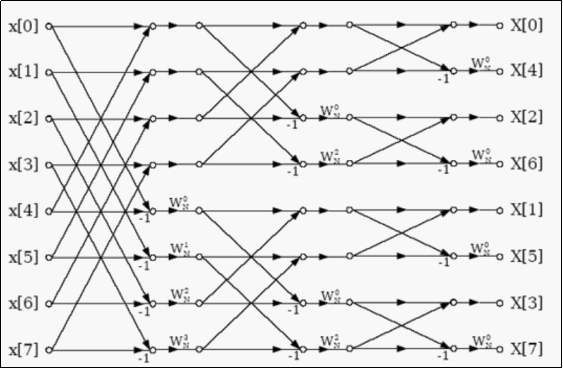
（上面这种图形就是蝴蝶变换，因为看起来有点像蝴蝶）

蝴蝶变换的用处在于，它给了我们一种自底向上的 DFT 实现方法。我们可以预处理出每一个下标的二进制反转，然后将下标和其二进制反转所保存的系数相交换，最后自底向上地合并。这种迭代版本比递归版本要更快、占用空间要更少。

还原：逆离散傅里叶变换

逆离散傅里叶变换（IDFT）是将 DFT 求出的点值表达还原为系数表达的方法（这个过程称为插值）。

这个过程看上去需要另一种专门的方法，但实际上不需要。我们设 为单位根 作为横坐标时，对应的点的纵坐标。那么显然有 。

然后结论是 。直接给出结论比较唐突（因为我也不知道这是怎么想出来的），我们可以验证一下：

先做和式变换，。若 $k=i$，则贡献为 ；否则固定 $k$，根据单位根性质，。所以式子成立。

这个结论的形式表明了我们可以按照 DFT 的方式来做 IDFT，只需要将代入的对象换成 ，并在最后将系数除以 $n$ 即可。

实现

下面给出一个迭代方法实现的模板。其中蝴蝶变换给出了两种实现方式。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
struct Comp{
    double rlt, img;
    Comp(double xx, double yy){
        rlt = xx, img = yy;
    }
    Comp(){
        rlt = img = 0;
    }
    Comp operator + (const Comp &ca){
        return Comp(rlt + ca.rlt, img + ca.img);
    }
    Comp operator - (const Comp &ca){
        return Comp(rlt - ca.rlt, img - ca.img);
    }
    Comp operator * (const Comp &ca){
        return Comp(rlt * ca.rlt - img * ca.img, rlt * ca.img + img * ca.rlt);
    }
};
double Pi = acos(-1.0);
int rev[250005];
void reverse_bit(int len){
    rev[0] = 0, rev[len - 1] = len - 1;
    int j = (len >> 1), k;
    for(int i = 1; i < len - 1; ++i){
        rev[i] = j, k = (len >> 1);
        for(; j >= k; j -= k, k >>= 1);
        j += k;
    }
}
void reverse_bit_2(int len){
    rev[0] = 0;
    for (int i = 1; i < len; ++i)
        rev[i] = (rev[i >> 1] >> 1) + ((i & 1) ? (len >> 1): 0);
}
void fft(Comp E[], int len, int opt){
    for(int i = 0; i < len; ++i)
        if(rev[i] > i) swap(E[i], E[rev[i]]);
    for(int h = 1; h < len; h <<= 1){
        Comp wn(cos(Pi / h), opt * sin(Pi / h));
        for(int i = 0; i < len; i += (h << 1)){
            Comp w(1, 0); 
            for(int j = 0; j < h; ++j, w = w * wn){
                Comp x = E[i + j], y = w * E[i + j + h];
                E[i + j] = x + y, E[i + j + h] = x - y;
            }
        }
    }
    if(opt == -1){
        for(int i = 0; i < len; ++i)
            E[i].rlt *= 1.0 / len;
    }
}

FFT 主程序中，设定交换两个值的条件为 rev[i] > i 是为了避免交换两次而抵消效果。参数 opt 为 1 表示当前做的是 DFT，为 -1 表示是 IDFT。

注意循环中单位根使用的角度是 $\frac{\pi}{h}$，因为 2 上下消去了。

NTT（快速数论变换）

FFT 能够解决大部分的问题，但是它的精度和速度都不够理想，而且有时候“运算对象必须是复数”这个条件会非常累赘。这一点尤其体现在只有整数参与运算的场合。

为此，我们希望有一个专门针对整数的卷积计算工具。这就是 NTT。

基本原理

回想一下，我们之所以要将复数作为运算对象，是因为我们要用单位根来求值，而使用单位根就必须使用复数。而在数论中，恰好有一个概念能提供和单位根一样具有良好的性质，那就是原根。

原根是和具体的模数相关的概念，这里我们取模数 $M=k2^t + 1$，其中 $2^t$ 很大，远大于 $n$。设 $M$ 的原根为 $g$。

然后定义模意义下的单位根，设 。容易验证，单位根的前 2 条性质在这里成立。我们验证其余 3 条性质：（注意，下面的计算都是模意义下进行的）

  1. 。前者显然，对后者，考虑 。由单位根互不相同可知 。
  2. 。只需注意 $g^{M-1} \equiv 1 \pmod M$。
  3. 。只需注意：利用等比数列求和可得分子为 。

由此可知，NTT 在整个代码结构上和 FFT 基本不会有太大区别，只需要在具体的计算上稍加修改即可。

实现

在这里，我们使用经典模数 998244353，原根选 3。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
const int M = 998244353, g = 3, invg = 332748118;
void ntt(int E[], int len, int opt){
    for(int i = 0; i < len; ++i)
        if(rev[i] > i) swap(E[i], E[rev[i]]); // 强制定序
    for(int h = 1, id = 0; h < len; h <<= 1, ++id){
        int wn = poww(opt == 1 ? g: invg, (M - 1) / (h << 1), M);
        for(int i = 0; i < len; i += (h << 1)){
            int w = 1;
            for(int j = 0; j < h; ++j, w = 1ll * w * wn % M){
                int x = E[i + j], y = 1ll * w * E[i + j + h] % M;
                E[i + j] = (x + y >= M ? x + y - M: x + y), 
                E[i + j + h] = (x + M - y >= M ? x - y: x + M - y);
            }
        }
    }
    if(opt == -1){
        int invn = poww(len, M - 2, M);
        for(int i = 0; i < len; ++i)
            E[i] = 1ll * E[i] * invn % M;
    }
}

注意在给 E[i + j] 和 E[i + j + h] 取模的时候不要先计算再取模，而是先判断然后直接得到取模后的结果。否则效率会慢上一倍左右。

FWT（快速沃尔什变换）