模板 高精度整数

发表于 | 分类于 |
字数统计: 565 字

高精度整数运算的模板。

为了节省空间，此处不将运算封装成为一个类。

字符串变为高精度数

高精度整数用的比较多的是将大数变成一个万进制数，用一个数组储存。数组的第一位为万进制数的长度。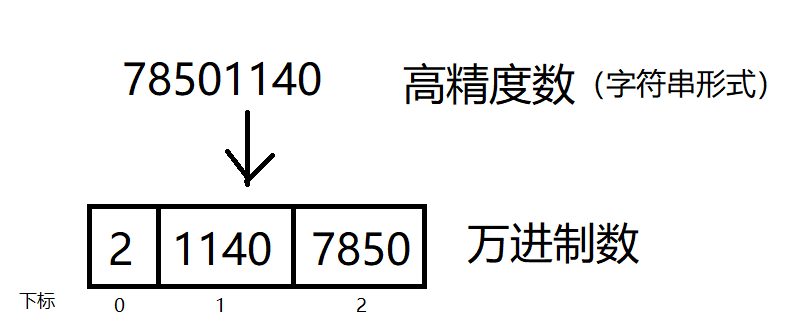
转换

1
2
3
4
5
6
7
8
9
10
11
int ten[] = {1, 10, 100, 1000};
inline void clearZero(int *bi){
    while(bi[0] && !bi[bi[0]]) --bi[0];
}
void build(char *src, int *dst){
    int len = strlen(src);
    dst[0] = (len - 1) / 4 + 1;
    for(int i = len - 1, j = 0; i >= 0; --i, ++j)
        dst[(j >> 2) + 1] = (src[i] - '0') * ten[j & 3];
    clearZero(dst);
}

高精度比较

和字符串比大小差不多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//前者小于后者？
bool cmp1(int *s1, int *s2){
    if(s1[0] != s2[0]) return s1[0] < s2[0];
    for(int i = s1[0]; i >= 1; --i)
        if(s1[i] != s2[i]) return s1[i] < s2[i];
    return false;
}
//小于等于
bool cmp2(int *s1, int *s2){
    if(s1[0] != s2[0]) return s1[0] < s2[0];
    for(int i = s1[0]; i >= 1; --i)
        if(s1[i] != s2[i]) return s1[i] < s2[i];
    return true;
}
//等于
bool cmp3(int *s1, int *s2){
    for(int i = 0; i <= s1[0]; ++i)
        if(s1[i] != s2[i]) return false;
    return true;
}

高精度加法

从最低位开始加，一直加到更大数的最高位。

1
2
3
4
5
6
7
void add(int *s1, int *s2, int *dst){
    int len = max(s1[0], s2[0]), x = 0;
    dst[0] = len;
    for(int i = 1; i <= len; ++i)
        x += s1[i] + s2[i], dst[i] = x % 10000, x /= 10000;
    if(x > 0) dst[++dst[0]] = x;
}

如果不支持不停的memset那就改写成这样：

1
2
3
4
5
6
7
8
9
10
11
12
void add(int *s1, int *s2, int *dst){
    int len1 = max(s1[0], s2[0]), len2 = s1[0] + s2[0] - len1, x = 0;
    dst[0] = len1;
    int *smax;
    if(s1[0] == len1) smax = s1;
    else smax = s2;
    for(int i = 1; i <= len2; ++i)
        x += s1[i] + s2[i], dst[i] = x % 10000, x /= 10000;
    for(int i = len2 + 1; i <= len1; ++i)
        x += smax[i], dst[i] = x % 10000, x /= 10000;
    if(x > 0) dst[++dst[0]] = x;
}

高精度减法

默认为$a-b$，因为负数不太好实现。

高精度乘法

乘一个小于10000的数

乘一个大数

高精度左移

直接执行对该数乘上2。

高精度幂

高精度除法

高精度开方

高精度GCD

直接使用Stein算法。
void gcd(int s1, int s2, int *dst){
dst[0] = dst[1] = 1;
}