普及T1 金币
模拟1
2
3
4
5
6
7
8
9
10
11
12
using namespace std;
int main(){
int k,ans=0;
scanf("%d",&k);
for(int i=1,j=1;i<=k;i++){
ans+=j;
if(j*(j+1)/2==i)j++;
}
printf("%d\n",ans);
return 0;
}
普及T2 扫雷游戏
模拟1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
using namespace std;
int n,m,mat[105][105],dx[]={-1,-1,-1,0,0,1,1,1},
dy[]={-1,0,1,-1,1,-1,0,1};
char s[105];
void get(int x,int y){
int res=0;
for(int i=0;i<8;i++)
res+=(mat[x+dx[i]][y+dy[i]]==-1);
mat[x][y]=res;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%s",s+1);
for(int j=1;j<=m;j++)
mat[i][j]-=(s[j]=='*');
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)
if(!mat[i][j])get(i,j),printf("%d",mat[i][j]);
else putchar('*');
putchar('\n');
}
return 0;
}
普及T3 求和
我们挖掘条件的性质可以发现:$y$无关紧要,当$x$和$z$的奇偶性相同时,他们之间旧就会产生分数。
所以每一种颜色分奇偶计数,然后一种颜色一个奇偶性产生的分数为
其中$s_4$为该种颜色该种奇偶性的格子数,$s_1$为这些格子$x\times num_x$的和,$s_2$和$s_3$分别为这些格子$x$和$num_x$的和。其中$x$指编号,$num_x$指编号为$x$的格子上的数。
证明过程略,可以自己手动推导。
综上,这个算法的时间复杂度是$O(n+m)$。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
using namespace std;
typedef long long ll;
int read(){
int f=1,x=0;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-f;c=getchar();}
while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();
return f*x;
}
int n,m,num[100005],col[100005],ans=0;
int s1[100005][2],s2[100005][2],s3[100005][2],s4[100005][2];
void init(){
n=read(),m=read();
for(int i=1;i<=n;i++)num[i]=read()%M;
for(int i=1;i<=n;i++)col[i]=read();
}
void solve(){
for(int i=1;i<=n;i++){
int c=col[i],B=i&1;
s1[c][B]+=i*num[i],s1[c][B]%=M;
s2[c][B]+=i,s2[c][B]%=M;
s3[c][B]+=num[i],s3[c][B]%=M;
s4[c][B]++;
}
for(int i=1;i<=m;i++)
for(int j=0;j<2;j++)
ans+=(s4[i][j]-2)*s1[i][j]%M,
ans+=s2[i][j]*s3[i][j]%M,
ans%=M;
printf("%d\n",ans);
}
int main(){
init();
solve();
return 0;
}
普及T4 推销员
一道贪心。
我们可以先算出总的疲劳值,然后每一次选择哪一户人家再也不去。这个时候,我们要保证减少的疲劳值最少。
我们可以发现一次只有$2$种删去住户的决策: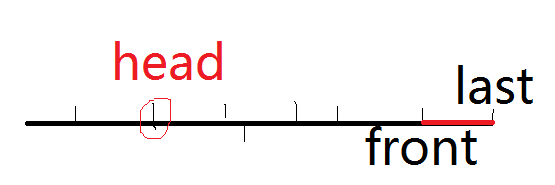
如图,$head$表示当前疲劳值消耗最小的住户编号,$last$表示最低端的住户编号,$front$是$last$前一个住户的编号。
每一次可以去掉$head$,也可以去掉$last$。而去掉$last$就没必要走$front$到$last$的路了,所以第二种决策会减少$(dis[last]-dis[front])\times 2+last$需要的疲劳值。
对住户的(疲劳值,编号)二元组按疲劳值排个序,然后维护以上3个量即可:$last$,$front$和$head$。
注意,还需要维护每一个住户是否已经被清除,是的话要打标记,否则$head$指向的住户可能会是$last$,这样就不合法。
时间复杂度:$O(nlogn)$1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
using namespace std;
int dis[M],cost[M][2],ans[M],tmp[M],front,t,n,last,head;
bool vis[M]={0};
int cmp(const void *a,const void *b){
return *(int*)a-*(int*)b;
}
int main(){
scanf("%d",&n);
int i;
for(i=0;i<n;i++)
scanf("%d",&dis[i]);
ans[n-1]=dis[n-1]*2;
for(i=0;i<n;i++)
scanf("%d",&tmp[i]),
cost[i][1]=i,
cost[i][0]=tmp[i],
ans[n-1]+=cost[i][0];
qsort(cost,n,sizeof(cost[0]),cmp);
last=n-1,front=n-2,head=0;
vis[last]=true;
for(i=n-2;i>=0;i--){
ans[i]=ans[i+1];
while(head<n&&(vis[cost[head][1]]))head++;
t=(dis[last]-dis[front])*2+tmp[last];
if(t<cost[head][0])
vis[last]=vis[front]=1,
ans[i]-=t,
last=front--;
else
vis[cost[head][1]]=1,
ans[i]-=cost[head][0],
head++;
while(vis[front])front--;
}
for(i=0;i<n;i++)
printf("%d\n",ans[i]);
return 0;
}
提高D1T1 神奇的幻方
模拟1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
using namespace std;
int n,ans[50][50]={0};
int main(){
scanf("%d",&n);
int i,j,x,y;
for(i=2,x=0,y=n/2,ans[x][y]=1;i<=n*n;i++){
if(!x){
if(y==n-1)x++;
else x=n-1,y++;
}else{
if(y==n-1)y=0,x--;
else {
if(!ans[x-1][y+1])
x--,y++;
else x++;
}
}
ans[x][y]=i;
}
for(i=0;i<n;i++,printf("\n"))
for(j=0;j<n;j++,(j<n)?printf(" "):0)
printf("%d",ans[i][j]);
return 0;
}
提高D1T2 信息传递
乱搞。
题目:求最小环。
解:爆搜/tarjan。
能用tarjan是因为这里面的强连通分量只能是简单环。
DFS解法
1 |
|
Tarjan解法
1 |
|
提高D1T3 斗地主
部分搜索。
先搞掉所有顺子,然后问题转化为一个简单的最优化问题,dp可解。
设$f(i,j,k,l)$为一副牌,有$i$份4张,$j$份3张,$k$份2张,$l$份1张,最少打几次。这个最开始就可以做。然后搜索即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
using namespace std;
typedef long long ll;
int read(){
int f=1,x=0;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-f;c=getchar();}
while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();
return f*x;
}
//剪枝:出牌数递减,(牌大小递增)
//贪心:5个直接搞
int n,cnt[20],ans;
int f[7][9][13][24],pat[5];
void dp(){//与顺子无关的dp
memset(f,0x3f,sizeof(f));
f[0][0][0][0]=0;
int xa=n/4,xb=n/3,xc=n/2;
for(int i=0;i<=xa;i++)
for(int j=0;j<=xb;j++)
for(int k=0;k<=xc;k++)
for(int l=0;l<=n;l++){
int &t=f[i][j][k][l];
if(i){
t=min(t,f[i-1][j][k][l]+1);
if(l>=2)t=min(t,f[i-1][j][k][l-2]+1);
if(k>=2)t=min(t,f[i-1][j][k-2][l]+1);
}
if(j){
t=min(t,f[i][j-1][k][l]+1);
if(l)t=min(t,f[i][j-1][k][l-1]+1);
if(k)t=min(t,f[i][j-1][k-1][l]+1);
}
if(k)t=min(t,f[i][j][k-1][l]+1);
if(l)t=min(t,f[i][j][k][l-1]+1);
}
}
int small_solve(){
for(int i=0;i<=4;i++)pat[i]=0;
for(int i=0;i<=13;i++)pat[cnt[i]]++;
return f[pat[4]][pat[3]][pat[2]][pat[1]];
}
void dfs(int cd,int st){
if(st+1>=ans&&cd!=0)return ;
if(cd==0){
ans=min(ans,st);
return ;
}
int flag=0;
//只搜索顺子
for(int k=1;k<=12;k++){
if(cnt[k]>=3){
if(k<=11){
for(int i=k+1;i<=12&&cnt[i]>=3;i++){
flag=1;
for(int j=k;j<=i;j++)cnt[j]-=3;
dfs(cd-(i-k+1)*3,st+1);
for(int j=k;j<=i;j++)cnt[j]+=3;
}
}
}
if(cnt[k]>=2){
if(k<=10&&cnt[k+1]>=2){
for(int i=k+2;i<=12&&cnt[i]>=2;i++){
flag=1;
for(int j=k;j<=i;j++)cnt[j]-=2;
dfs(cd-(i-k+1)*2,st+1);
for(int j=k;j<=i;j++)cnt[j]+=2;
}
}
}
if(cnt[k]){
if(k<=8&&cnt[k+1]&&cnt[k+2]&&cnt[k+3]){
for(int i=k+4;i<=12&&cnt[i];i++){
flag=1;
for(int j=k;j<=i;j++)cnt[j]--;
dfs(cd-(i-k+1),st+1);
for(int j=k;j<=i;j++)cnt[j]++;
}
}
}
}
ans=min(ans,st+small_solve());
}
void init(){
ans=n;
memset(cnt,0,sizeof(cnt));
int u;
for(int i=1;i<=n;i++){
u=read();
if(!u)cnt[u]++;
else if(u<=2)cnt[u+11]++;
else cnt[u-2]++;
read();
}
}
void solve(){
dfs(n,0);
printf("%d\n",ans);
}
int main(){
int T=read();
n=read();
dp();
while(T--){
init();
solve();
}
return 0;
}
提高D2T1 跳石头
看到描述就看的出是二分答案。
二分答案,设为$x$,把石头排序之后扫一遍,看看是否有石头与前一个石头的间隔小于$x$,有的话拆掉该石头,否则把这个石头作为“前一个石头”,再看下一个。如果拆的次数大于$M$就判定失败,否则判定成功。
时间复杂度$O(NlogL)$。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
using namespace std;
typedef long long ll;
int read(){
int f=1,x=0;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-f;c=getchar();}
while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();
return f*x;
}
int L,n,m,at[50005];
bool C(int x){
int left=m,lst=0;
for(int i=2;i<=n+2;i++){
if(at[i]-lst<x)left--;
else lst=at[i];
if(left<0)return 0;
}
return 1;
}
void init(){
L=read(),n=read(),m=read();
at[1]=0,at[n+2]=L;
for(int i=2;i<=n+1;i++)
at[i]=read();
sort(at+2,at+n+2);
}
void solve(){
int l=0,r=L,mid;
while(r>l){
mid=(l+r+1)>>1;
if(C(mid))l=mid;
else r=mid-1;
}
printf("%d\n",l);
}
int main(){
init();
solve();
return 0;
}
提高D2T2 子串
看数据范围猜算法系列
时间复杂度相信各位都看的出来:$O(nmk)$
怎么刻画状态呢?
首先有$2$维必不可缺:$i$表示$A$前$i$个字符,$j$表示$B$前$j$个字符。这里指的是用前$i$个$A$的字符来匹配$B$的前$j$个字符,串$A$的前$i$个不一定要严格匹配,但串$B$的前$j$个必须严格匹配上。
之后,段也要表示:$t$表示现在做了$t$段。
看到这些段不是连续的,所以使用情况也要表示出来,设一个布尔变量$l$表示串$A$的这个字符是不是被使用了,是为$1$,不是为$0$。
够了,用$f(i,j,t,l)$来表示。
不使用这个字符,就继承串$A$上一位的状态。使用的话,必须匹配成功,然后有$2$个决策:开启新的一段(前一个字符没用的话就默认开启新的一段了),或者接上前一段。
得到状态转移方程:
初始是$f(i,0,0,0)=1$。
要用滚动数组,不然MLE。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
using namespace std;
int n,m,k,dp[2][205][205][2]={0},ans=0,M=1000000007;
char a[1005]={0},b[205]={0};
int main(){
scanf("%d%d%d%s%s",&n,&m,&k,&a[1],&b[1]);
int i,j,o,p,t;
dp[0][0][0][0]=dp[1][0][0][0]=1;
for(i=1;i<=n;i++){
for(j=1;j<=m;j++){
for(o=1;o<=k;o++){
if(a[i]==b[j])
dp[i&1][j][o][1]=((
dp[1^(i&1)][j-1][o-1][0]+
dp[1^(i&1)][j-1][o][1])%M+
dp[1^(i&1)][j-1][o-1][1])%M;
else dp[i&1][j][o][1]=0;
dp[i&1][j][o][0]=(
dp[1^(i&1)][j][o][0]+//
dp[1^(i&1)][j][o][1])%M;
}
}
}
printf("%d\n",(dp[n&1][m][k][0]+dp[n&1][m][k][1])%M);
return 0;
}
提高D2T3 运输计划
直接求解显然很困难,考虑转化为判定性问题,二分一个答案$x$,判定他是否可行。
完成一次运输的时间取决于最长路的大小,也就是保证所有路径的长度都小于$x$。考虑大于$x$的路径,在他们的公共路上删掉一段路才可以使他们一起变小。理所当然的,这段路必须是他们的公共路径中最长的一段。
怎么找这条最长的公共路呢?我们可以玩一玩区间加法,给每一个在$(u,v)$两点上的路径打一个标记,这样就说明这些点在$(u,v)$路径上。如果两点的标记数都等于长度大于$x$的路径总数,呢么两点间的这段路就是他们的公共路径。
区间加法有$2$种实现方式:一种是树剖/$LCT$,一种是树上差分(和序列上的没区别)。由于只需要查询一遍,没必要用什么奇奇怪怪的数据结构,所以用差分,在$x$和$y$上打一个$+1$标记,在$LCA$处打一个$-2$标记。由于是对点操作,所以要把边和点捆绑起来。具体不难实现。
时间复杂度取决于求解$LCA$时所用算法的时间复杂度。用倍增的时间复杂度是$O((n+m)logn)$。
注意卡常。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
using namespace std;
typedef struct{
int v,cost,_next;
}Edge;
Edge edge[MAXN*2];
int n,m,par[MAXN][20]={0},dis[MAXN]={0},cnt=0,at[MAXN];
int son[MAXN]={0},bro[MAXN]={0},depth[MAXN];
int bus[MAXN][4],_dis[MAXN];// 0 路径长 1 _dis 到父亲的路径长
int dec[MAXN]={0},que[MAXN],f,r,sum[MAXN];
int cmp(const void *a,const void *b){
return *(int*)b-*(int*)a;//从大到小
}
void addedge(int _u,int _v,int _cost){
edge[cnt].v=_v,
edge[cnt].cost=_cost,
edge[cnt]._next=at[_u],
at[_u]=cnt++;
}
int read(){
int x=0;char c=getchar();
while(c<'0'||c>'9')c=getchar();
while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();
return x;
}
int bs(int lth){
int s=0,len=m,md,pos;
while(len){
md=s+(len>>1);
if(lth<bus[md][0])
s=md+1,len=len-(len>>1)-1;
else len>>=1;
}
return s;
}
void _init(){
int i,j,h,u,v,c;
f=r=0;
que[r++]=1,depth[1]=1;
while(r-f){
h=que[f++];
for(i=at[h];i!=-1;i=edge[i]._next){
v=edge[i].v;
if(v==par[h][0])continue;
que[r++]=v,
depth[v]=depth[h]+1,
par[v][0]=h,
bro[v]=son[h],son[h]=v,
_dis[v]=edge[i].cost,
dis[v]=dis[h]+_dis[v];
}
for(i=1;i<=19;i++)
if(par[h][i-1])
par[h][i]=par[par[h][i-1]][i-1];
else break;
}
}
int query(int u,int v){
int i,j;
if(depth[u]<depth[v])
swap(u,v);
for(i=0;(1<<i)<=depth[u]-depth[v];i++);
for(i--;i>=0&&depth[u]!=depth[v];i--)
if(depth[u]-(1<<i)>=depth[v])
u=par[u][i];
if(u==v)return u;
for(i=19;i>=0;i--)
if(par[u][i]>0&&par[u][i]!=par[v][i])
u=par[u][i],v=par[v][i];
return par[u][0];
}
int C(int tot){
int i,j,h,maxi=0,_max=0;
for(i=r-1;i>=0;i--){
h=que[i];
for(sum[h]=dec[h],j=son[h];j;j=bro[j])
sum[h]+=sum[j];
if(sum[h]>maxi)
maxi=sum[h],_max=_dis[h];
else if(sum[h]==maxi)
_max=max(_max,_dis[h]);
}
return maxi==tot?_max:0;
}
void prepare(){
n=read(),m=read();
int i,j,u,v,c;
memset(at,-1,sizeof(at));
for(i=0;i<n-1;i++)
u=read(),v=read(),c=read(),
addedge(u,v,c),
addedge(v,u,c);
_init();
for(i=0;i<m;i++)
u=read(),v=read(),
bus[i][1]=u,bus[i][2]=v,
bus[i][3]=query(u,v),
bus[i][0]=dis[u]+dis[v]-2*dis[bus[i][3]];
}
void solve(){
qsort(bus,m,sizeof(bus[0]),cmp);
int s=max(0,bus[m-1][0]-1001),t=bus[0][0],md,i,w;
while(t-s){
md=(t+s)/2;
memset(dec,0,sizeof(dec));
for(i=0;i<m&&bus[i][0]>md;i++)
dec[bus[i][1]]++,
dec[bus[i][2]]++,
dec[bus[i][3]]-=2;
w=C(i);
if(bus[0][0]-w<=md)t=md;
else s=md+1;
}
printf("%d\n",s);
}
int main(){
prepare();
solve();
return 0;
}