斐波那契系列问题

我不会数学orz

基础

斐波那契数列定义式：

$F(0) = 0, F(1) = 1, F(n) = F(n+1)+F(n+2) \quad (n\ge 2)$

通项公式是$F(n)=\frac{1}{\sqrt 5} \left[\left(\frac{1+\sqrt 5}{2} \right)^n - \left(\frac{1-\sqrt 5}{2}\right)^n\right]$。这个通项公式可以通过数列的特征方程或对矩阵求特征值得到。
因为这个定义式也是一个线性齐次递推，所以也可以用矩阵来表示，写成

$\begin{bmatrix} F(n) \\ F(n - 1) \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} F(n - 1) \\ F(n - 2) \end{bmatrix}$

意义

斐波那契数列可以表示很多意义，即等价表示。

生兔子

这个例子太经典了，跳过。

爬楼梯

有$n-1$阶楼梯，每次可以爬1阶或者2阶，求总共上楼梯方法数。
由递推易知答案为$F(n)$。而由排列组合容易知答案是 $\sum _{i = 0} ^{\lfloor \frac{n-1}{2} \rfloor} \tbinom{n-1-i}{n-1-2i} = \sum _{i = 0} ^{\lfloor \frac{n-1}{2} \rfloor} \tbinom{n-1-i}{i}$ 。所以有

$F(n)=\sum _{i = 0} ^{\lfloor \frac{n-1}{2} \rfloor} \tbinom{n-1-i}{i} \quad (n>0)$

用途

分解$\phi ^n$

其中$\phi = \frac{1+\sqrt 5}{2}$。因为$\phi^2 = \phi + 1$，因此可以把$\phi$的高次幂反复用这个式子，分解成$\phi$和$1$的线性组合。用归纳可以证明$\phi^n = F(n)\phi + F(n-1)$。

证明辗转相除法复杂度

拉梅就是用了斐波那契数列证明了辗转相除法的时间复杂度是$O(\log n)$级别的。即Lame’s theorem。

性质

判定一个数是否是斐波那契数

对通项公式解方程可以得出

$n=\log _{\phi} \left( \frac{\sqrt 5F(n) + \sqrt{5F^2(n) \pm 4}}{2}\right)$

因此$x$是斐波那契数$\iff$$5x^2+4$或者$5x^2-4$是完全平方数。

广义斐波那契数列

首先看一个喜闻乐见的题目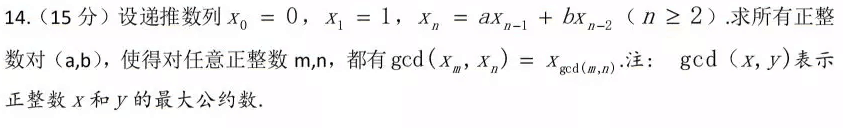

（题目来源于中科大）
答案：只要$\gcd (a, b) = 1$即可。下面对此进行证明：
先证： $\gcd(b, x_n) = 1 (n\ge 1) \quad (1)$
证明：用归纳，对于$n=1$显然成立。假设对于$n=k(k\ge 1)$成立，对于$n=k+1$：
有 $\gcd(x_{k+1}, b)=\gcd(ax_{k}+bx_{k-1},b)=\gcd(ax_{k},b))=1$ 。证毕。

再证： $\gcd(x_n, x_{n-1})=1 (n\ge 2)\quad (2)$
证明：用归纳，对于$n=2$显然成立。假设对于$n=k(k\ge 2)$成立，对于$n=k+1$：
有 $\gcd(x_{k+1}, x_k) = \gcd(ax_k+bx_{k-1}, x_k) = \gcd(bx_{k-1}, x_k) \overset{(1)}{=} \gcd(x_{k-1}, x_k)=1$ 。证毕。

再证： $x_{m+n}=x_mx_{n+1}+bx_{m-1}x_n(m, n\in \mathbb{N}) \quad (3)$
证明：

$\begin{aligned} x_{m+n} &= ax_{m+n-1}+bx_{m+n-2} \\ &= x_2x_{m+n-1}+bx_1x_{m+n-2} \\ &= (ax_2+bx_1)x_{m+n-2}+bx_2x_{m+n-3} \\ &= x_3x_{m+n-2} + bx_2x_{m+n-3} \\ &= \cdots = x_{i+1}x_{m+n-i}+bx_ix_{m+n-i-1}\end{aligned}$

令$i=n$有 $x_{m+n}=x_mx_{n+1}+bx_{m-1}x_n$ 。证毕。

因此：

$\begin{aligned} \gcd(x_{m+n},x_n) &\overset{(3)}{=} \gcd(x_mx_{n+1}+bx_{m-1}x_n, x_n) \\ &= \gcd(x_mx_{n+1}, x_n) \\ &\overset{(2)}{=} \gcd(x_m, x_n) \end{aligned}$

相当于对$x$的下标做更相减损。
所以最后的答案即为$x_{\gcd(m,n)}$。

若$\gcd(a, b)> 1$，那么 $\gcd(x_2, x_3)\neq x_1$ 。
从而上述条件的充分性和必要性满足，证毕。

斐波那契的模问题

古代人的难题要写。

参考材料：

维基百科