HNOI2013 数列

发表于 | 分类于 |
字数统计: 723 字

题目链接

题解

这题我用了一种不够数学的方法来解。
30分做法：
DP，设$f(i,j)$表示第$i$天以$j$为当天股价的方案数，则

答案为$\sum_{j=1}^N f(K,j)$
数据太大，只能拿30分。
100分做法：
在30分做法上做文章。
可以发现，对于所有$i\le N-(K-1)M$的$f(0,i)$而言，他们对最终答案的贡献是一样的。
（因为他们可以给出的贡献的上界都是$i+(K-1)M$，下界都是$i+K-1$）
但对于更大的$i$，由于要求的答案范围的上界为$N$，所以他们对更高股价的贡献是要去掉的。
问题转化为求$N-(K-1)M$个相同的贡献值的和以及$(K-1)M$个不同贡献值的和。
对于前一个子问题，我们考虑一个等价的问题：
从第一个格子出发，每一个格子有$M$条路通向下一个格子，问走$K-1$步的走法数，一种走法和另外一种走法相同当且仅当两条路径完全相同。
由乘法原理知答案为$M^{K-1}$。
所以前一个子问题的答案为$[N-(K-1)M]M^{K-1}$。
后一个子问题不好办。怎么弄？
假设，画图，观察。（这是我的方法，当然有其他方法发现这个规律。）
设$M=3,K=4$，则作图：
1
（$i$表示天数，这张表表示开始的某个$f(1,j)$对后面第$i$天答案的贡献）
然后依次写出$j=N-(K-1)M+1,N-(K-1)M+2,…,N-(K-1)$时对答案的贡献。
（$j>N-(K-1)$时，$j$对答案贡献为$0$。）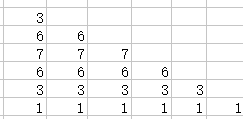
2
这是个很对称的图形，沿对角线翻折后发现每一列都变为了完整的一列。
一列的和我们之前已经求了出来，就是$M^{K-1}$。
设其内部所有数的和为$sum$，则

总答案即为

使用快速幂和逆元计算即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cstring>
#include <cctype>
#define INF 2000000000
using namespace std;
typedef long long ll;
ll N,M,K,P;
ll Pow(ll a,ll b,ll c){
    ll res=1;
    a%=c;
    while(b){
        if(b&1)res=(res*a)%c;
        a=(a*a)%c,b>>=1;
    }
    return res;
}
int read(){
    int f=1,x=0;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-f;c=getchar();}
    while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();
    return f*x; 
}	
void init(){
    scanf("%lld%lld%lld%lld",&N,&K,&M,&P);
}
void solve(){
    ll ans1=Pow(M,K-1,P);
    ll inv2,ans;
    N%=P,ans=(N*ans1)%P;
    if(M&1)inv2=(M+1)/2,inv2=inv2*M%P;
    else inv2=M/2,inv2=inv2*(M+1)%P;
    inv2=inv2*(K-1)%P;
    inv2=inv2*Pow(M,K-2,P)%P;
    ans+=P,ans=(ans-inv2)%P;
    printf("%lld\n",ans);
}
int main(){
    init();
    solve();
    return 0;
}

Powered By Valine
v1.5.2