题解
给出一种这个题的思考方法吧…
设$f(i,j)$表示$i$维超立方体中$j$维元素的个数。
先思考:点的个数如何变化?
很显然,每升一维,点的个数就多一倍,故$f(i,0)=2^i$。
而根据规律可以看出,某一维在升维之后,他自己这一维复制了一份,同时原来比他小一维德元素也升为了他这一维。
故得到递推关系:$f(i,j)=2f(i-1,j)+f(i-1,j-1)$。
结合以上两个方程,很容易想到这是一个$O(n^2)$的dp。
但显然不行。这么做复杂度大的太可怕。
可以发现,这个递推模型和杨辉三角很像。所以我们写一下: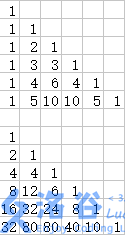
观察发现,每一斜列都构成一个高阶等差数列。
换言之,第$q$个斜列上的数都可以表示成一个$q-1$次多项式。
计算后可以发现,对于同样的$q$,右边的第$k$个位置的数总是比左边的同样位置的数大$2^{q-1}$倍。
根据这个就可以发现,下面每一个数的通项为
所以答案就是。
之后组合数取模什么的拿线性逆元做即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
using namespace std;
typedef long long ll;
ll a,b,inv[100005];
ll q_pow(ll a,ll b){
ll res=1;
while(b){
if(b&1)res=(res*a)%P;
a=(a*a)%P,b>>=1;
}
return res;
}
void init(){
scanf("%lld%lld",&a,&b);
}
void solve(){
if(a<b){
printf("0\n");
return ;
}//特判
inv[1]=1;
for(ll i=2;i<=100000;i++)
inv[i]=(P-(P/i))*inv[P%i]%P;//逆元
ll ans=q_pow(2,a-b);
for(int i=1;i<=b;i++)
ans=ans*(a-i+1)%P,
ans=ans*inv[i]%P;
printf("%lld\n",ans);
}
int main(){
init();
solve();
return 0;
}